- Define \( x\diamond y \) to be \( \left| {x - y}\right| \) for all real numbers \( x \) and \( y \) . What is the value of \( \left( {1\diamond \left( {2\diamond 3}\right) }\right) - \left( {\left( {1\diamond 2}\right) \diamond 3}\right) ? \)
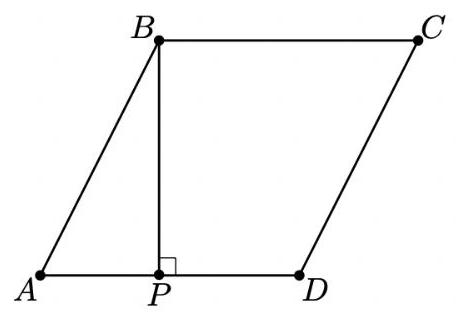
- In rhombus \( {ABCD} \) , point \( P \) lies on segment \( \overline{AD} \) so that \( \overline{BP} \bot \overline{AD},{AP} = 3 \) , and \( {PD} = 2 \) . What is the area of \( {ABCD} \) ? (Note: The figure is not drawn to scale.)
- How many three-digit positive integers have an odd number of even digits?
- A donkey suffers an attack of hiccups and the first hiccup happens at 4:00 one afternoon. Suppose that the donkey hiccups regularly every 5 seconds. At what time does the donkey's 700th hiccup occur?
- What is the value of the below expression?
对于所有的实数 \( x \) 和 \( y, x\diamond y \) 定义为 \( \left| {x - y}\right| \) . 问 \( \left( {1\diamond \left( {2\diamond 3}\right) }\right) - \left( {\left( {1\diamond 2}\right) \diamond 3}\right) \) 的值是多少?
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
(F) Leave as blank | 不作答
在菱形 \( {ABCD} \) 中,点 \( P \) 位于线段 \( \overline{AD} \) 上使得 \( \overline{BP} \bot \overline{AD},{AP} = 3,{PD} = 2 \) . 问 \( {ABCD} \) 的面积是多少?(注:图形未按比例绘制.)
(A) \( 3\sqrt{5} \)
(B) 10
(C) \( 6\sqrt{5} \)
(D) 20
(E) 25
(F) Leave as blank | 不作答 2022 MAA AMC 10B
包含奇数个偶数数码的三位正整数有多少个?
(A) 150
(B) 250
(C) 350
(D) 450
(E) 550
(F) Leave as blank | 不作答
一头驴因病连续打嗝,第一次打嗝发生在下午 4:00. 假设驴每隔 5 秒打嗝一
次. 那么驴第 700 次打嗝发生在什么时间?
(A) 15 seconds after 4:58 | 4:58 之后的 15 秒
(B) 20 seconds after 4:58 | 4:58 之后的 20 秒
(C) 25 seconds after 4:58 | 4:58 之后的 25 秒
(D) 30 seconds after 4:58 | 4:58 之后的 30 秒
(E) 35 seconds after 4:58 | 4:58 之后的 35 秒
(F) Leave as blank | 不作答
下面表达式的值是多少?
\[ \frac{\left( {1 + \frac{1}{3}}\right) \left( {1 + \frac{1}{5}}\right) \left( {1 + \frac{1}{7}}\right) }{\sqrt{\left( {1 - \frac{1}{{3}^{2}}}\right) \left( {1 - \frac{1}{{5}^{2}}}\right) \left( {1 - \frac{1}{{7}^{2}}}\right) }} \]
(A) \( \sqrt{3} \)
(B) 2
(C) \( \sqrt{15} \)
(D) 4
(E) \( \sqrt{105} \)
(F) Leave as blank | 不作答
2022 MAA AMC 10B
- How many of the first ten numbers of the sequence 121, 11211, 1112111, ... are prime numbers?
- For how many values of the constant \( k \) will the polynomial \( {x}^{2} + {kx} + {36} \) have two distinct integer roots?
- Consider the following 100 sets of 10 elements each:
在数列 121, 11211, 1112111, ... 的前十项中有多少个数是素数?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
(F) Leave as blank | 不作答
使得多项式 \( {x}^{2} + {kx} + {36} \) 有两个不同的整数根的常数 \( k \) 的取值有多少种?
(A) 6
(B) 8
(C) 9
(D) 14
(E) 16
(F) Leave as blank | 不作答
2022 MAA AMC 10B
\[ \{ 1,2,3,\ldots ,{10}\} \text{,} \]
\[ \{ {11},{12},{13},\ldots ,{20}\} \text{,} \]
\[ \{ {21},{22},{23},\ldots ,{30}\} \text{,} \]
\( \vdots \)
\[ \{ {991},{992},{993},\ldots ,{1000}\} \text{.} \]
How many of these sets contain exactly two multiples of 7 ?
考虑以下的 100 个集合,每个集合中有 10 个元素:
\[ \{ 1,2,3,\ldots ,{10}\} \text{,} \]
\[ \{ {11},{12},{13},\ldots ,{20}\} \text{,} \]
\[ \{ {21},{22},{23},\ldots ,{30}\} \text{,} \]
\[ \{ {991},{992},{993},\ldots ,{1000}\} \]
在这些集合中, 恰好包含两个 7 的倍数的集合有多少个?
(A) 40
(B) 42
(C) 43
(D) 49
(E) 50
(F) Leave as blank | 不作答
- The sum
\[ \frac{1}{2!} + \frac{2}{3!} + \frac{3}{4!} + \cdots + \frac{2021}{{2022}!} \]
can be expressed as \( a - \frac{1}{b!} \) , where \( a \) and \( b \) are positive integers. What is
\( a + b \) ?
和式
\[ \frac{1}{2!} + \frac{2}{3!} + \frac{3}{4!} + \cdots + \frac{2021}{{2022}!} \]
可以表达成 \( a - \frac{1}{b!} \) 的形式,其中 \( a \) 和 \( b \) 是正整数. 问 \( a + b \) 的值是多少?
(A) 2020
(B) 2021
(C) 2022
(D) 2023
(E) 2024
(F) Leave as blank | 不作答
- Camila writes down five positive integers. The unique mode of these integers is 2 greater than their median, and the median is 2 greater than their arithmetic mean. What is the least possible value for the mode?
- All the high schools in a large school district are involved in a fundraiser selling T-shirts. Which of the choices below is logically equivalent to the statement "No school bigger than Euclid HS sold more T-shirts than Euclid HS”?
- A pair of fair 6-sided dice is rolled \( n \) times. What is the least value of \( n \) such that the probability that the sum of the numbers face up on a roll equals 7 at least once is greater than \( \frac{1}{2} \) ?
- The positive difference between a pair of primes is equal to 2 , and the positive difference between the cubes of the two primes is equal to 31106 . What is the sum of the digits of the least prime that is greater than those two primes?
- Suppose that \( S \) is a subset of \( \{ 1,2,3,\ldots ,{25}\} \) such that the sum of any two (not necessarily distinct) elements of \( S \) is never an element of \( S \) . What is the maximum number of elements \( S \) may contain?
- Let \( {S}_{n} \) be the sum of the first \( n \) terms of an arithmetic sequence that has a common difference of 2 . The quotient \( \frac{{S}_{3n}}{{S}_{n}} \) does not depend on \( n \) . What is \( {S}_{20} \) ?
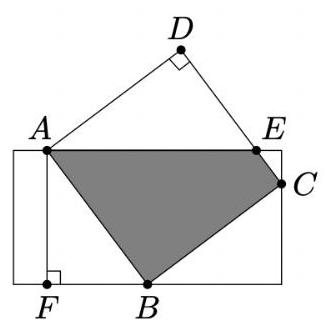
- The diagram below shows a rectangle with side lengths 4 and 8 and a square with side length 5 . Three vertices of the square lie on three different sides of the rectangle, as shown. What is the area of the region inside both the square and the rectangle?
- One of the following numbers is not divisible by any prime number less than 10. Which is it?
- Consider systems of three linear equations with unknowns \( x, y \) , and \( z \) ,
Camila 写下了五个正整数. 这些整数的唯一众数比它们的中位数大 2 , 而中位数比它们的算术平均数大 2. 问众数的最小可能值是多少?
(A) 5
(B) 7
(C) 9
(D) 11
(E) 13
(F) Leave as blank | 不作答
2022 MAA AMC 10B
(A) All schools smaller than Euclid HS sold fewer T-shirts than Euclid HS.
(B) No school that sold more T-shirts than Euclid HS is bigger than Euclid HS.
(C) All schools bigger than Euclid HS sold fewer T-shirts than Euclid HS.
(D) All schools that sold fewer T-shirts than Euclid HS are smaller than Euclid HS.
(E) All schools smaller than Euclid HS sold more T-shirts than Euclid HS.
一个很大的学区的所有高中都参与了一项出售 \( \mathrm{T} \) 恤的筹款活动. 以下哪个选项在逻辑上等同于陈述 “没有比 Euclid 高中更大的学校卖出了比 Euclid 高中更多的 T 恤”
(A) 所有比 Euclid 高中更小的学校都卖出比 Euclid 高中更少的 T 恤.
(B) 没有比 Euclid 高中卖出更多的 \( \mathrm{T} \) 恤的学校比 Euclid 高中更大.
(C) 所有比 Euclid 高中更大的学校都卖出比 Euclid 高中更少的 T 恤.
(D) 所有卖出比 Euclid 高中更少的 T 恤的学校都比 Euclid 高中更小.
(E) 所有比 Euclid 高中更小的学校都卖出比 Euclid 高中更多的 T 恤.
(A) A
(B) \( \mathrm{B} \)
(C) C
(D) D
(E) \( \mathrm{E} \)
(F) Leave as blank | 不作答
2022 MAA AMC 10B
一对公平的 6 个面的骰子被抛掷 \( n \) 次. 如果至少有一次掷出的两个数之和等于 7 的概率大于 \( \frac{1}{2} \) ,那么 \( n \) 的最小值是多少?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
(F) Leave as blank | 不作答
一对素数之间形成的是正数的差等于 2 , 这两个素数的立方之间形成的是正数的差等于 31106. 问大于这两个素数的最小素数的各位数字之和是多少?
(A) 8
(B) 10
(C) 11
(D) 13
(E) 16
(F) Leave as blank | 不作答
2022 MAA AMC 10B
设 \( S \) 是 \( \{ 1,2,3,\ldots ,{25}\} \) 的子集,使得 \( S \) 中的任何两个(不一定互异)元素的总和不是 \( S \) 中的元素. 问 \( S \) 中最多可以包含多少个元素?
(A) 12
(B) 13
(C) 14
(D) 15
(E) 16
(F) Leave as blank | 不作答
设 \( {S}_{n} \) 是一个公差为 2 的等差数列的前 \( n \) 项之和. 商 \( \frac{{S}_{3n}}{{S}_{n}} \) 的值不依赖于 \( n \) . 问 \( {S}_{20} \) 是多少?
(A) 340
(B) 360
(C) 380
(D) 400
(E) 420
(F) Leave as blank | 不作答
2022 MAA AMC 10B
下图显示了一个长为 8 ,宽为 4 的矩形以及一个边长为 5 的正方形. 如图所示,正方形的三个顶点位于矩形的三条不同的边上. 问正方形和矩形公共部分的面积是多少?
(A) \( {15}\frac{1}{8} \)
(B) \( {15}\frac{3}{8} \)
(C) \( {15}\frac{1}{2} \)
(D) \( {15}\frac{5}{8} \)
(E) \( {15}\frac{7}{8} \)
(F) Leave as blank | 不作答
下列各数中有一个数不能被任何小于 10 的素数整除. 问这是哪个数?
(A) \( {2}^{606} - 1 \)
(B) \( {2}^{606} + 1 \)
(C) \( {2}^{607} - 1 \)
(D) \( {2}^{607} + 1 \)
(E) \( {2}^{607} + {3}^{607} \)
(F) Leave as blank | 不作答
2022 MAA AMC 10B
\[ {a}_{1}x + {b}_{1}y + {c}_{1}z = 0 \]
\[ {a}_{2}x + {b}_{2}y + {c}_{2}z = 0 \]
\[ {a}_{3}x + {b}_{3}y + {c}_{3}z = 0 \]
where each of the coefficients is either 0 or 1 and the system has a solution other than \( x = y = z = 0 \) . For example, one such system is \( \langle {1x} + {1y} + \) \( {0z} = 0,{0x} + {1y} + {1z} = 0,{0x} + {0y} + {0z} = 0\rangle \) with a nonzero solution of \( \left( {x, y, z}\right) = \left( {1, - 1,1}\right) \) . How many such systems of equations are there? (The equations in a system need not be distinct, and two systems containing the same equations in a different order are considered different.)
考虑由三个线性方程组成的,未知数为 \( x, y \) 和 \( z \) 的方程组:
\[ {a}_{1}x + {b}_{1}y + {c}_{1}z = 0 \]
\[ {a}_{2}x + {b}_{2}y + {c}_{2}z = 0 \]
\[ {a}_{3}x + {b}_{3}y + {c}_{3}z = 0 \]
其中的每个系数为 0 或 1,并且方程组有除去 \( x = y = z = 0 \) 之外的解. 例如, 一个这样的方程组是 \( \langle {1x} + {1y} + {0z} = 0,{0x} + {1y} + {1z} = 0,{0x} + {0y} + {0z} = 0\rangle \) , 它有非零解 \( \left( {x, y, z}\right) = \left( {1, - 1,1}\right) \) . 问共有多少个这样的方程组? (一个方程组中的方程允许是相同的, 并且两个包含同样的方程, 但排列顺序不同的方程组被认为是不同的.)
(A) 302
(B) 338
(C) 340
(D) 343
(E) 344
(F) Leave as blank | 不作答
2022 MAA AMC 10B
- Each square in a \( 5 \times 5 \) grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
- Any filled square with two or three filled neighbors remains filled.
- Any empty square with exactly three filled neighbors becomes a filled square.
- All other squares remain empty or become empty.
- 任何有两个或三个相邻的方格是灰色的灰色方格继续保持是灰色的.
- 任何恰好有三个相邻的方格是灰色的空白方格将成为灰色方格.
- 所有其他的方格要么继续保持是空白的, 要么变成空白方格.
- Let \( {ABCD} \) be a rhombus with \( \angle {ADC} = {46}^{ \circ } \) . Let \( E \) be the midpoint of \( \overline{CD} \) , and let \( F \) be the point on \( \overline{BE} \) such that \( \overline{AF} \) is perpendicular to \( \overline{BE} \) . What is the degree measure of \( \angle {BFC} \) ?
- Let \( P\left( x\right) \) be a polynomial with rational coefficients such that when \( P\left( x\right) \) is divided by the polynomial \( {x}^{2} + x + 1 \) , the remainder is \( x + 2 \) , and when \( P\left( x\right) \) is divided by the polynomial \( {x}^{2} + 1 \) , the remainder is \( {2x} + 1 \) . There is a unique polynomial of least degree with these two properties. What is the sum of the squares of the coefficients of that polynomial?
- Let \( S \) be the set of circles that are tangent to each of the three circles in the coordinate plane whose equations are \( {x}^{2} + {y}^{2} = 4,{x}^{2} + {y}^{2} = {64} \) , and \( (x - \) \( 5{)}^{2} + {y}^{2} = 3 \) . What is the sum of the areas of all the circles in \( S \) ?
- Ant Amelia starts on the number line at 0 and crawls in the following manner. For \( n = 1,2,3 \) , Amelia chooses a time duration \( {t}_{n} \) and an increment \( {x}_{n} \) independently and uniformly at random from the interval(0,1). During the \( n \) th step of the process, Amelia moves \( {x}_{n} \) units in the positive direction, using up \( {t}_{n} \) minutes. If the total elapsed time has exceeded 1 minute during the \( n \) th step, she stops at the end of that step; otherwise, she continues with the next step, taking at most 3 steps in all. What is the probability that Amelia's position when she stops will be greater than 1 ?
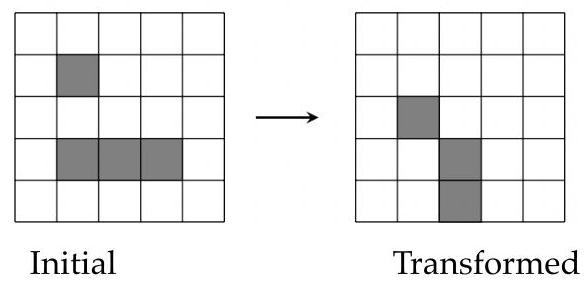
A sample transformation is shown in the figure below.
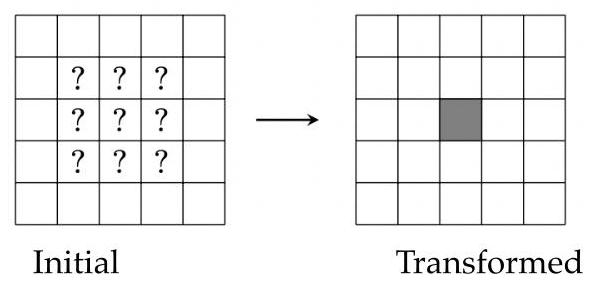
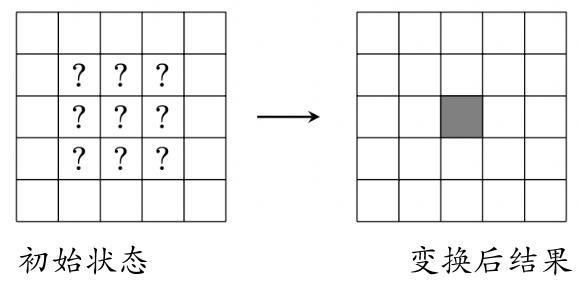
Suppose the \( 5 \times 5 \) grid has a border of empty squares surrounding a \( 3 \times 3 \) subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
2022 MAA AMC 10B
\( 5 \times 5 \) 方格表中的每个方格要么是灰色的,要么是空白的,并且最多有八个相邻的方格, 这里有公共边或者公共顶点的方格认为是相邻的. 方格表按以下规则进行转换:
下图显示了一个转换的示例.
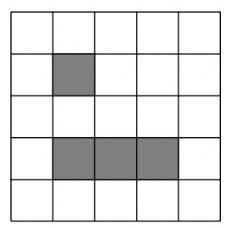
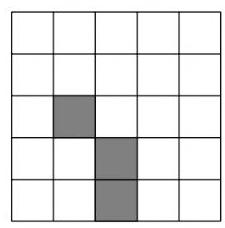
初始状态 变换后结果
假设 \( 5 \times 5 \) 方格表周界上的方格都是空白的,它们围绕着中间的 \( 3 \times 3 \) 子方格表. 那么经过一次转换后, 方格表变为只有中心方格是灰色的初始构型有多少个? (一个构型经过旋转和反射后而形成的构型被认为是不同的.)
(A) 14
(B) 18
(C) 22
(D) 26
(E) 30
(F) Leave as blank | 不作答
2022 MAA AMC 10B
在菱形 \( {ABCD} \) 中, \( \angle {ADC} = {46}^{ \circ } \) . 设 \( E \) 为 \( \overline{CD} \) 的中点,而 \( F \) 为 \( \overline{BE} \) 上的点, 使得 \( \overline{AF} \) 垂直于 \( \overline{BE} \) . 问 \( \angle {BFC} \) 的度数是多少?
(A) 110
(B) 111
(C) 112
(D) 113
(E) 114
(F) Leave as blank | 不作答
设 \( P\left( x\right) \) 是一个有理系数的多项式,使得当 \( P\left( x\right) \) 除以多项式 \( {x}^{2} + x + 1 \) 时, 余式为 \( x + 2 \) ,而当 \( P\left( x\right) \) 除以多项式 \( {x}^{2} + 1 \) 时,余式为 \( {2x} + 1 \) . 满足上述两个条件的次数最低的多项式是唯一的. 问该多项式的各项系数的平方和是多少?
(A) 10
(B) 13
(C) 19
(D) 20
(E) 23
(F) Leave as blank | 不作答
2022 MAA AMC 10B
设 \( S \) 是坐标平面中,与方程为 \( {x}^{2} + {y}^{2} = 4,{x}^{2} + {y}^{2} = {64},{\left( x - 5\right) }^{2} + {y}^{2} = 3 \) 的三个圆中的每一个都相切的圆组成的集合. 问 \( S \) 中所有圆的面积之和是多少?
(A) \( {48\pi } \)
(B) \( {68\pi } \)
(C) \( {96\pi } \)
(D) \( {102\pi } \)
(E) \( {136\pi } \)
(F) Leave as blank | 不作答
蚂蚁 Amelia 在数轴上从 0 开始,按以下方式爬行. 对于 \( n = 1,2,3 \) , Amelia 从区间(0,1)中随机独立且均匀地选择持续时间 \( {t}_{n} \) 和步长 \( {x}_{n} \) . 在爬行过程的第 \( n \) 步, Amelia 沿正向移动 \( {x}_{n} \) 个单位,用时 \( {t}_{n} \) 分钟. 如果在第 \( n \) 步移动期间,所经过的总时间超过 1 分钟,则她在该步结束时停止;否则,她会继续下一步,最多一共走 3 步. 问 Amelia 停止在大于 1 的数所对应的位置处的概率是多少?
(A) \( \frac{1}{3} \)
(B) \( \frac{1}{2} \)
(C) \( \frac{2}{3} \)
(D) \( \frac{3}{4} \)
(E) \( \frac{5}{6} \)
(F) Leave as blank | 不作答 24. Consider functions \( f \) that satisfy
\[ \left| {f\left( x\right) - f\left( y\right) }\right| \leq \frac{1}{2}\left| {x - y}\right| \]
for all real numbers \( x \) and \( y \) . Of all such functions that also satisfy the equa-
tion \( f\left( {300}\right) = f\left( {900}\right) \) , what is the greatest possible value of
\[ f\left( {f\left( {800}\right) }\right) - f\left( {f\left( {400}\right) }\right) \text{?} \]
考虑具有以下性质的函数 \( f \) : 对于所有的实数 \( x \) 和 \( y \) ,
\[ \left| {f\left( x\right) - f\left( y\right) }\right| \leq \frac{1}{2}\left| {x - y}\right| . \]
在所有这样的函数中,如果还要求满足等式 \( f\left( {300}\right) = f\left( {900}\right) \) ,那么
\[ f\left( {f\left( {800}\right) }\right) - f\left( {f\left( {400}\right) }\right) \]
的最大可能值是多少?
(A) 25
(B) 50
(C) 100
(D) 150
(E) 200
(F) Leave as blank | 不作答
2022 MAA AMC 10B
- Let \( {x}_{0},{x}_{1},{x}_{2},\ldots \) be a sequence of numbers, where each \( {x}_{k} \) is either 0 or 1 . For each positive integer \( n \) , define
\[ {S}_{n} = \mathop{\sum }\limits_{{k = 0}}^{{n - 1}}{x}_{k}{2}^{k} \]
Suppose \( 7{S}_{n} \equiv 1\left( {\;\operatorname{mod}\;{2}^{n}}\right) \) for all \( n \geq 1 \) . What is the value of the sum
\[ {x}_{2019} + 2{x}_{2020} + 4{x}_{2021} + 8{x}_{2022}? \]
在数列 \( {x}_{0},{x}_{1},{x}_{2},\ldots \) 中,每个 \( {x}_{k} \) 均为 0 或 1 . 对于每个正整数 \( n \) ,定义
\[ {S}_{n} = \mathop{\sum }\limits_{{k = 0}}^{{n - 1}}{x}_{k}{2}^{k} \]
假设对所有 \( n \geq 1 \) ,有 \( 7{S}_{n} \equiv 1\left( {\;\operatorname{mod}\;{2}^{n}}\right) \) . 问和式
\[ {x}_{2019} + 2{x}_{2020} + 4{x}_{2021} + 8{x}_{2022} \]
的值是多少?
(A) 6
(B) 7
(C) 12
(D) 14
(E) 15
(F) Leave as blank | 不作答
2022 MAA AMC 10B
Answers.
ADDAB ABBDD BCEBD DCBCD EECBA